What are tetra- and polychoric correlations?

Polychoric correlations estimate the correlation between two theorized normal distributions given two ordinal variables. In psychological research, much of our data fits this definition. For example, many survey studies used with introductory psychology pools use Likert scale items. The responses to these items typically range from 1 (Strongly disagree) to 6 (Strongly agree). However, we don’t really think that person’s relationship to the item is actually polytomous. Instead, it’s an imperfect approximation.

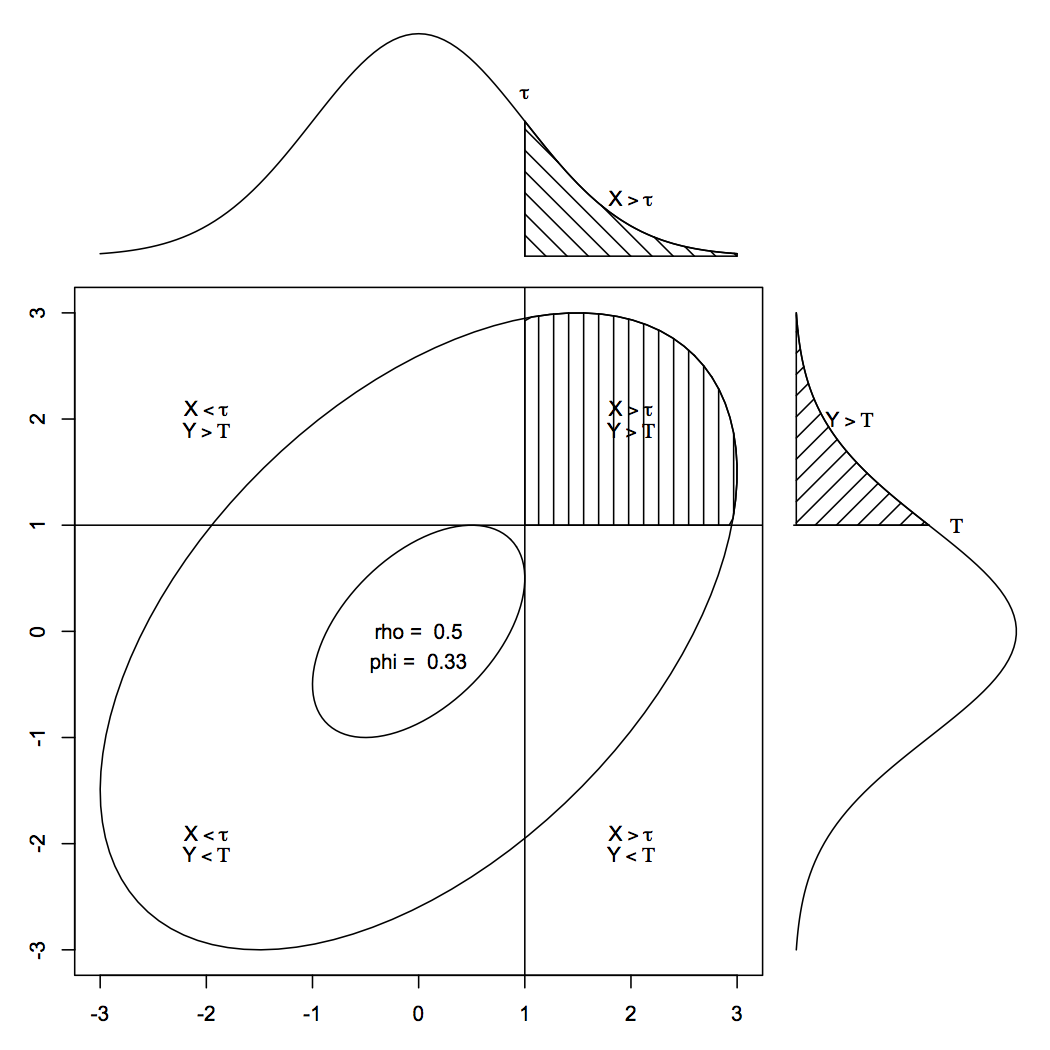
Similarly, tetrachorics are special cases of polychoric crrelations when the variable of interest is dichotomous. The participant may have gotten the item either correct (i.e., 1) or incorrect (i.e., 0), but the underlying knowledge that led to the items’ response is probably a continuous distribution.

When you have polytomous rating scales but want to disattenuate the correlations to more accurately estimate the correlation betwen the latent continuous variables, one way of doing this is to use a tetrachoric or polychoric correlation coefficient.

The problem

At the SAPA Project, the majority of our data is polytomous. We ask you the degree to which you like to go to lively parties to estimate your score on latent extraversion. Presently, we use mixed.cor(), which calls a combination of the tetrachoric() and polychoric() functions in the psych package (Revelle, W., 2013).

However, each time we build a new dataset from the website’s SQL server, it takes hours. And that’s if everything goes well. If there’s an error in the code or a bug in a new function, it may take hours to hit the error, wasting your day.

After a bit of profiling, it was revealed that much of our time building the SAPA dataset was used estimating the tetrachoric and polychoric correlation coefficients. When you do this for 250,000+ participants for 10,000+ variables, it takes a long time. So Bill and I thought about how we could speed them up and feel others may benefit from our optimization.

A serious speedup to tetrachoric and polychoric was initiated with the help of Bill Revelle. The increase in speed is roughly 1- (nc-1)² / nc² where nc is the number of categories. Thus, for tetrachorics where nc=2, this is a 75% reduction, whereas for polychorics of 6 item responses this is just a 30% reduction.

Optimizing the existing function

If we call psych:::tetraBinBvn, we see that most of the time spent computer the tetrachorics is using pmvnorm to estimate each of the 4 probabilities of the tetrachoric:

The function says for each row i and each column j, optimize a probability based on the lower and upper bounds of the row cuts and column cuts. But wait! Since the sum of the probabilities in the tetrachoric 2x2 matrix add to 1, why not just use a bit of subtraction to figure it out? That would avoid waiting on pvnorm to compute each cell.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function (rho, rc, cc)
{
    row.cuts <- c(-Inf, rc, Inf)
    col.cuts <- c(-Inf, cc, Inf)
    P <- matrix(0, 2, 2)
    R <- matrix(c(1, rho, rho, 1), 2, 2)
    for (i in 1:2) {
        for (j in 1:2) {
            P[i, j] <- pmvnorm(lower = c(row.cuts[i], col.cuts[j]),
                upper = c(row.cuts[i + 1], col.cuts[j + 1]),
                corr = R)
        }
    }
    P
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

function (rho, rc, cc)
{
    row.cuts <- c(-Inf, rc, Inf)
    col.cuts <- c(-Inf, cc, Inf)
    P <- matrix(0, 2, 2)
    R <- matrix(c(1, rho, rho, 1), 2, 2)
    P[1, 1] <- pmvnorm(lower = c(row.cuts[1], col.cuts[1]), upper = c(row.cuts[2],
        col.cuts[2]), corr = R)
    P[1, 2] <- pnorm(rc) - P[1, 1]
    P[2, 1] <- pnorm(cc) - P[1, 1]
    P[2, 2] <- 1 - pnorm(rc) - P[2, 1]
    P
}
<environment: namespace:psych>

This solution resulted in a speed up of tetrachor() by a factor of 3!

Unfortunately, our trick doesn’t work for the polychor() function as well, since there are more degrees of freedom. However, we can eliminate calling pvnorm() for 11 cells in a hypothetical 6x6 matrix as we only need to find the values for 25 and can use subtraction to speed up the estimation of the remaining 11. This results in a less impressive speed up for polychor() that I nonetheless hope will benefit researchers.

Writing a parallelized function

While we were happy with our initial speed increase, it didn’t have a noticeable impact on SAPA’s build time. We then began to explore ways to parallelize our existing code. While we attempted to use various packages (i.e., foreach), we settled on using mcmapply in the existing core parallel library to minimize our dependencies.

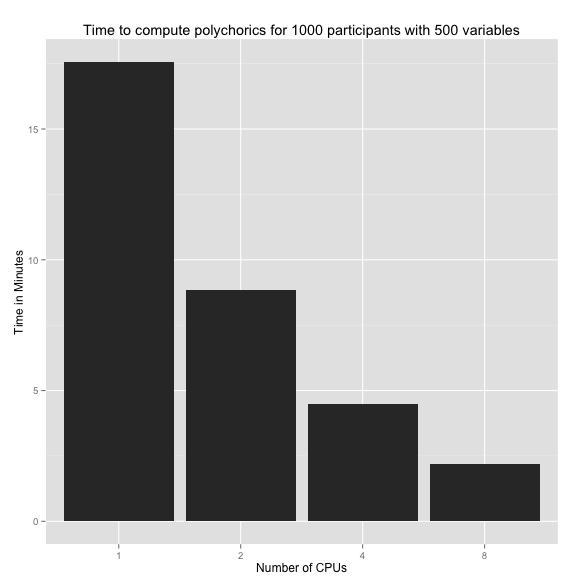
As you can see below, this resulted in a speed increase by a factor of N, where N = # of cpus you allocate. Be warned, however, that memory consumption increases dramatically as well.