Jason A. French

Northwestern University

Repeated Measures in R

In this tutorial, I’ll cover how to analyze repeated-measures designs using 1) multilevel modeling using the lme package and 2) using Wilcox’s Robust Statistics package (see Wilcox, 2012). In a repeated-measures design, each participant provides data at multiple time points. Due to this, the assumptions about model error are different for variances which are presented between subjects (i.e., SSB than are variables presented within subjects (i.e., SSW. After the within-subject variability is partialled out, we model separately the effect of the experiment (i.e., SSE and the error not account for by the experiment (i.e., SSR).

When using this tutorial, there are a few things to keep in mind:

  1. This is a draft. I’ll be updating this page with more graphs and explanations as time allows, informed by your feedback.

  2. Multilevel models and Robust ANOVAs are just a few of the ways that repeated-measures designs can be analyzed. I’ll be presenting the multilevel approach using the nlme package because assumptions about sphericity are different and are less of a concern under this approach (see Field et al., 2012, p. 576).

One way repeated measures

The first dataset we’ll be using can be obtained from the Personality Project:

Reading the dataset
1
2

data <- read.table(file = "http://personality-project.org/r/datasets/R.appendix3.data",
    header = T)

The main research question is does the valence of the word affect the rate at which items are recalled? First, let’s take a look at descriptive statistics of the dataset. We can sort them by the item valence using the describeBy() function in the psych package, which is available on CRAN.

Generating descriptive statistics by a group
1
2
3
4
5

# Load the psych package
library(psych)

# Describe the Recall variable by the Valence variable
describeBy(data$Recall, group = data$Valence)
Generating descriptive statistics by a group
1
2
3
4
5
6
7
8
9
10
11

## group: Neg
##   var n mean  sd median trimmed  mad min max range  skew kurtosis   se
## 1   1 5 27.8 3.9     29    27.8 4.45  22  32    10 -0.39    -1.72 1.74
## -------------------------------------------------------- 
## group: Neu
##   var n mean  sd median trimmed  mad min max range  skew kurtosis   se
## 1   1 5 11.6 2.7     12    11.6 2.97   8  15     7 -0.09    -1.83 1.21
## -------------------------------------------------------- 
## group: Pos
##   var n mean   sd median trimmed  mad min max range skew kurtosis  se
## 1   1 5   40 3.81     40      40 2.97  35  45    10    0    -1.78 1.7

Graphing the Effect

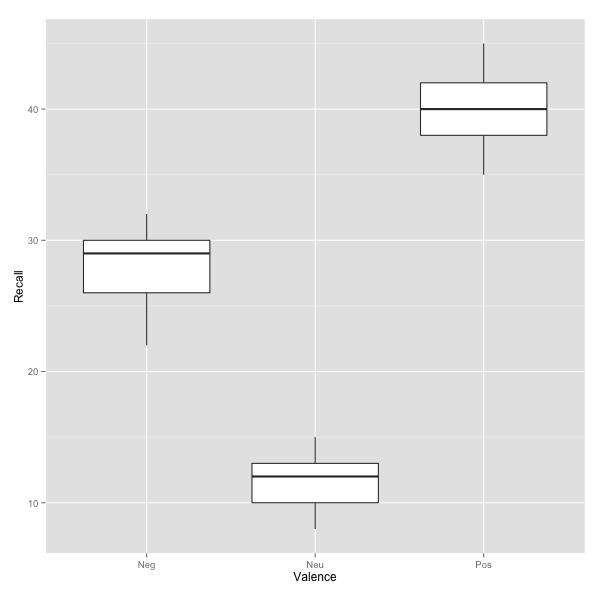
We can generate a quick boxplot to display the effect of Valence on Recall using the ggplot2 pacakge from CRAN.

1
2

library(ggplot2)
qplot(Valence, Recall, data=data, geom="boxplot")

Multilevel Approach

A multilevel model is simply a regression that allows for the errors to be dependent on eachother (as our conditions of Valence were repeated within each participant). To run this type of analysis, we’ll use the nlme package from CRAN, although I’ve also had good luck with the lme4 package if you like experimenting.

Installing nlme
1

install.packages('nlme')

Similar to any approach to model testing, we want to see if our predictive, augmented model is better than a simple, 1 parameter mean model. Thus, we begin by specifying a baseline model in which the DV, Recall, is predicted by its overall mean. Second, we specify our model of interest, in which Recall is predicted instead by a the item Valence, which was repeated within subjects.

Specifying our 2 Models
1
2
3
4
5
6
7
8
9

# Load the nlme package
library(nlme)

# Compact Model
baseline <- lme(Recall ~ 1, random = ~1 | Subject/Valence, data = data, method = "ML")

# Augmented Model
valenceModel <- lme(Recall ~ Valence, random = ~1 | Subject/Valence, data = data,
    method = "ML")

One way of assessing the significance of our model is by comparing it from the baseline model. By comparing the models, we ask whether Valence as a predictor is significantly better than the simple mean model (i.e., a better fit). We can do this with the anova() function.

Comparing the Models
1

anova(baseline, valenceModel)
Comparing the Models
1
2
3

##              Model df    AIC    BIC logLik   Test L.Ratio p-value
## baseline         1  4 125.24 128.07 -58.62                       
## valenceModel     2  6  84.36  88.61 -36.18 1 vs 2   44.87  <.0001

The output contains a few indicators of model fit. Generally with AIC (i.e., Akaike information criterion) and BIC (i.e., Bayesian information criterion), the lower the number the better the model, as it implies either a more parsimonious model, a better fit, or both. The likelihood ratio indicates that our valenceModel is a significnatly better fit for the data than our baseline model (p < 0.0001). Therefore, the item Valence had a significant impact on the measured Recall of the participant, Χ2(2) = 44.87, p < 0.0001.

We can obtain more specific details about the model using the summary() function:

1

summary(valenceModel)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

## Linear mixed-effects model fit by maximum likelihood
##  Data: data 
##     AIC   BIC logLik
##   84.36 88.61 -36.18
## 
## Random effects:
##  Formula: ~1 | Subject
##         (Intercept)
## StdDev:       2.361
## 
##  Formula: ~1 | Valence %in% Subject
##         (Intercept) Residual
## StdDev:       1.886   0.8574
## 
## Fixed effects: Recall ~ Valence 
##             Value Std.Error DF t-value p-value
## (Intercept)  27.8     1.571  8  17.701       0
## ValenceNeu  -16.2     1.465  8 -11.057       0
## ValencePos   12.2     1.465  8   8.327       0
##  Correlation: 
##            (Intr) ValncN
## ValenceNeu -0.466       
## ValencePos -0.466  0.500
## 
## Standardized Within-Group Residuals:
##     Min      Q1     Med      Q3     Max 
## -0.6604 -0.2588  0.0889  0.2135  0.6316 
## 
## Number of Observations: 15
## Number of Groups: 
##              Subject Valence %in% Subject 
##                    5                   15

Post-Hoc Tests

Using multcomp for post-hoc tests
1
2
3

library(multcomp)
posthoc <- glht(valenceModel, linfct = mcp(Valence = "Tukey"))
summary(posthoc)
Using multcomp for post-hoc tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

## 
##    Simultaneous Tests for General Linear Hypotheses
## 
## Multiple Comparisons of Means: Tukey Contrasts
## 
## 
## Fit: lme.formula(fixed = Recall ~ Valence, data = data, random = ~1 | 
##     Subject/Valence, method = "ML")
## 
## Linear Hypotheses:
##                Estimate Std. Error z value Pr(>|z|)    
## Neu - Neg == 0   -16.20       1.31  -12.36   <2e-16 ***
## Pos - Neg == 0    12.20       1.31    9.31   <2e-16 ***
## Pos - Neu == 0    28.40       1.31   21.67   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## (Adjusted p values reported -- single-step method)

Thus, our post hoc analysis shows that participants’ rate of recall was significantly better for positively valenced items (M = 40) than neutral (M = 11.6, b = 28.40, p < .0001) and negatively valenced items (M = 27.8, b = 12.20, p < .0001). Similarly, neutral items were recalled at a significantly higher rate than negatively valenced items (b = -16.20, p < .0001).

Wilcox’s Robust ANOVA

As of 5/1/13, the WRS package must be compiled from source to be installed. You can obtain the source package from the R-Forge repo below:

1
2
3

install.packages(c('MASS', 'akima', 'robustbase'))
install.packages('WRS', repos='http://R-Forge.R-project.org',
               type='source')

Unlike using lme() to analyze the data as a multilevel model, rmanova() requires that the data are in wide format. To adjust our table, we’ll use the reshape2 package from CRAN and cast the data into a wide format.

Casting the data into wide format
1
2
3

install.packages('reshape2')
library(reshape2)
data.wide <- dcast(data, Subject ~ Valence, value.var = "Recall")

For some reason, the rmanova() function doesn’t like dealing with factors variables, so we’ll remove the 5 Subjects. Finally, we’ll use rmanova(), which trims the data by 20% before estimating the effect.

Running a robust ANOVA
1
2
3

library(WRS)
data.wide <- data.wide[, -1]
rmanova(data.wide)
Running a robust ANOVA
1
2

## [1] "The number of groups to be compared is"
## [1] 3
Running a robust ANOVA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

## $test
## [1] 154.7
## 
## $df
## [1] 1.263 2.527
## 
## $siglevel
## [1] 0.002402
## 
## $tmeans
## [1] 28.33 11.67 40.00
## 
## $ehat
## [1] 0.5631
## 
## $etil
## [1] 0.6317

Similar to our findings from above, Valence had a significant influence on the item recall rate of the participant, F(1.26, 2.52) = 154.66, p < .01. However, we still want to conduct post-hoc analysis on the 20% trimmed means, which we’ll do using the rmmcp() function.

Post-Hoc Analysis
1

rmmcp(data.wide)
Post-Hoc Analysis
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

## $n
## [1] 5
## 
## $test
##      Group Group    test  p.value p.crit    se
## [1,]     1     2  13.064 0.005808 0.0250 1.225
## [2,]     1     3  -5.814 0.028334 0.0500 2.236
## [3,]     2     3 -25.065 0.001588 0.0169 1.130
## 
## $psihat
##      Group Group psihat ci.lower ci.upper
## [1,]     1     2  16.00    6.632   25.368
## [2,]     1     3 -13.00  -30.103    4.103
## [3,]     2     3 -28.33  -36.979  -19.687
## 
## $con
##      [,1]
## [1,]    0
## 
## $num.sig
## [1] 3

Post-hoc analysis confirms that Negatively valenced items are significantly different from both Neutral (Ψ̂ = 16, p < .01) and Positive items (Ψ̂ = -13, p < .05). Additionally, Neutral items are significantly different from positive items (Ψ̂ = -28.33, p < .01).

Two way repeated measures ( In Progress)

The second dataset we’ll be using can be obtained from the Personality Project:

Reading the dataset
1
2

data.2 <- read.table(file = "http://personality-project.org/r/datasets/R.appendix4.data",
    header = T)

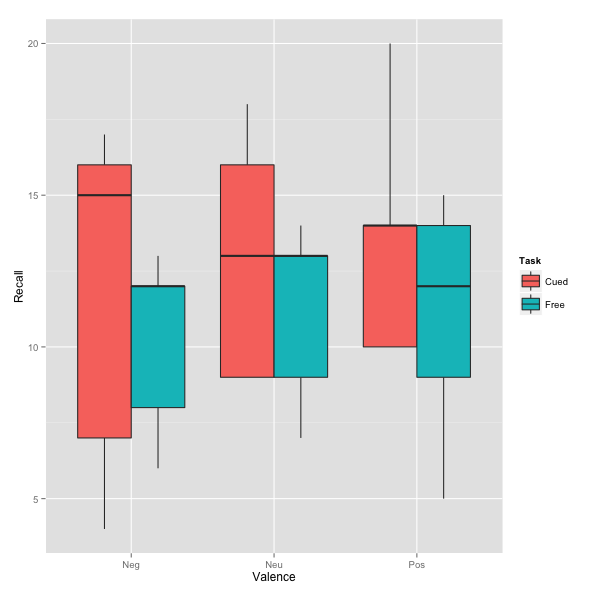
Graphing the Two-Way Interaction

Using ggplot2 to graph a boxplot
1
2

p <- ggplot(data.2, aes(Valence, Recall))
p + geom_boxplot(aes(fill = Task)

Multilevel Approach

Specifying our Models
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# Load the nlme package
library(nlme)

# Compact Model
baseline <- lme(Recall ~ 1, random = ~1 | Subject/Valence/Task, data = data.2, method = "ML")

valenceModel <- lme(Recall ~ Valence, random = ~1 | Subject/Valence/Task, data = data.2,
    method = "ML")

taskModel <- lme(Recall ~ Valence + Task, random = ~1 | Subject/Valence/Task, data = data.2,
    method = "ML")

fullModel <- lme(Recall ~ Valence * Task, random = ~1 | Subject/Valence/Task, data = data.2,
    method = "ML")

We again the significance of our models by comparing them from the baseline model. We can do this with the anova() function.

Comparing the Models
1

anova(baseline, valenceModel, taskModel, fullModel)
Comparing the Models
1
2
3
4
5

         Model df      AIC      BIC    logLik   Test  L.Ratio p-value
baseline         1  5 151.9240 158.9300 -70.96201
valenceModel     2  7 153.4414 163.2498 -69.72069 1 vs 2 2.482632  0.2890
taskModel        3  8 145.7924 157.0020 -64.89621 2 vs 3 9.648959  0.0019
fullModel        4 10 149.2138 163.2258 -64.60692 3 vs 4 0.578584  0.7488

References

  • Field, A., Miles, J., & Field, Z. (2012). Discovering Statistics Using R. SAGE Publications.

  • Wilcox, R. R. (2012). Introduction to robust estimate and hypothesis testing.

Comments